2021福建事业单位职测备考：熟练掌握方法，轻松解决数列构造问题

　　福建事业单位招聘网同步未知考试动态信息发布：2021福建事业单位职测备考：熟练掌握方法，轻松解决数列构造问题关注厦门华图微信公众号（xmhuatu），获取更多招考信息和备考资料。事业单位培训咨询电话：13110597044。添加客服小姐姐微信（xmhtxiaolai）获取更多电子材料和精美图书。

　　数列构造通常考查的是一种极端构造的解题思维，利用极值解题，就需要熟练掌握构造的思路和技巧。这类题目解题套路也是非常的固定，掌握技巧和思路其实很简单。首先我们需要大家知道这种题型的题型特征：问题中出现“最多……最多/少……”、“最少……最多/少……”、“排名第几……最多/少……”时。

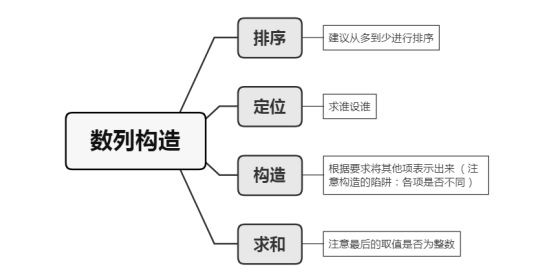
　　解题方法：排序——定位——构造——求和。接下来我们通过3道题来给大家详细说明这种题的解题思路和技巧。

　　【例1】现有21本故事书要分给5个人阅读，如果每个人得到的数量均不相同，那么得到故事书数量最多的人至少可以得到( )本。

　　A.5 B.7

　　C.9 D.11

　　【答案】B

　　【解析】第一步，识别题型，问题中出现“最多……最少……”特征，考查数列构造;

　　第二步，按照“排序——定位——构造——求和”四步解题，

　　排序：每个人得到故事书的数量均不相同，按照分得的故事书数量多少从多到少排序，就有1、2、3、4、5名;

　　定位：求谁设谁，根据问题“得到故事书数量最多的人至少可以得到多少本?”则让求的是得到故事书数量最多的人即求第一名有多少本，则设第一名为x本;

　　构造：根据要求将其他项表示出来，让求“得到故事书数量最多的人至少可以得到多少本?”即让第1名x最少，则让2、3、4、5名最多，第2名比第1名要少，则第2名最多比第1名少一本，为(x-1),第3名最多为(x-2),第4名最多为(x-3),第5名最多为(x-4);列表如下：

名次	1	2	3	4	5
数量	x	x-1	x-2	x-3	x-4

　　求和：根据总的书本数为21，可得x+(x-1)+(x-2)+(x-3)+(x-4)=21，解得x=6.2，即x至少为6.2，x为整数，所以得到故事书数量最多的人至少可以得到7本。

　　因此，选择B选项。

　　【例2】在一次竞标中，评标小组对参加竞标的公司进行评分，满分120分，按得分排名，前5名的平均分为115分，且得分是互不相同的整数，则第三名得分至少是( ) 。

　　A. 112分 B. 113分

　　C. 115分 D. 116分

　　【解析】第一步，识别题型，问题中出现“第几名……最少……”特征，考查数列构造;

　　第二步，按照“排序——定位——构造——求和”四步解题，

　　排序：每个人得分是互不相同的整数，按照得分的多少从多到少进行排序，就有1、2、3、4、5名;

　　定位：求谁设谁，根据问题“第三名得分至少是多少?”则让求的是第三名的得分，则设第三名得分为x;

　　构造：根据要求将其他项表示出来，让求“第三名得分至少是多少?”即让第3名x最少，则让1、2、4、5名都最多，第1名得分最多为满分120分，则第2名最多比第1名少一分119分,第4名最多比第三名少一分，为(x-1),第5名最多为(x-2);列表如下：

名次	1	2	3	4	5
得分	120	119	x	x-1	x-2

　　求和：根据前5名的平均分为115分，可得总得分为115×5，可得120+119+x+(x-1)+(x-2)=115×5，解得x=113，所以第三名得分至少为113分。

　　因此，选择B选项。

　　【例3】某单位2011年招聘了65名毕业生，拟分配到该单位的7个不同部门。假设行政部门分得的毕业生人数比其他部门都多，问行政部门分得的毕业生人数至少为多少名( )

　　A.10 B.11

　　C.12 D.13

　　【解析】第一步，识别题型，问题中出现“最多……最少……”特征，考查数列构造;

　　第二步，按照“排序——定位——构造——求和”四步解题，

　　排序：总共65名毕业生分到7个不同的部门，按照每个部门分的人数从多到少进行排序，就有1、2、3、4、5、6、7名;

　　定位：求谁设谁，根据问题“行政部门分得的毕业生人数至少为多少名?”行政部门分得的毕业生人数比其他部门都多，则让求的是第一名的得分，则设第一名得分为x;

　　构造：根据要求将其他项表示出来，让求“行政部门分得的毕业生人数至少为多少名?”即让第1名x最少，则让2、3、4、5、6、7名都最多，第2名人数最多比第1名少1人为(x-1)，这里要特别注意第3名到第7名的人数，题目中只说了行政部门分得的毕业生人数比其他部门都多，并没有说每个部门的人数都不同，所以第3名人数最多可以和第2名一样，为(x-1),同理，第4名人数最多可以和第3名一样，为(x-1),第4名人数最多可以和第3名一样，为(x-1),第5名人数最多可以和第4名一样，为(x-1),第6名人数最多可以和第5名一样，为(x-1),第7名人数最多可以和第6名一样，为(x-1),列表如下：

名次	1	2	3	4	5	6	7
人数	x	x-1	x-1	x-1	x-1	x-1	x-1

　　求和：根据总人数65人，可得x+(x-1)+(x-1)+(x-1)+(x-1)+(x-1)+(x-1)=65，解得x≈10.1，即x至少为10.1，x为整数，所以行政部门分得的毕业生人数至少为11人。

　　因此，选择B选项。

　　总结：从以上三个题目我们可以看到，数列构造的题型特征非常明显，解题套路同样非常固定，大家按照“排序——定位——构造——求和”四步解题，熟练掌握解题思路，另外在构造这一步要特别注意各项是否相同这个陷阱，最后的取值也要注意是否必须为整数，避免出现错误，数列构造考场上短时间内得分还是比较容易的。

　　本文地址：http://xiamen.huatu.com/2021/0712/1868725.html

（编辑：厦门华图黄老师）